下記条件で設計・計算例を提示します。
件:コイル内径 19mm以上
アーム長さ1(荷重点) 50mm
アーム長さ2(固定点) 50mm
荷重 32N
自由角度 90度
使用角度 45度
荷重条件 巻き込む方向
アーム形状 ストレート
外気に触れる、またばねの表面処理を特に行わないという事で材質はばね用ステンレス鋼線を選択しました。
下記表にて設計した事例を示します。
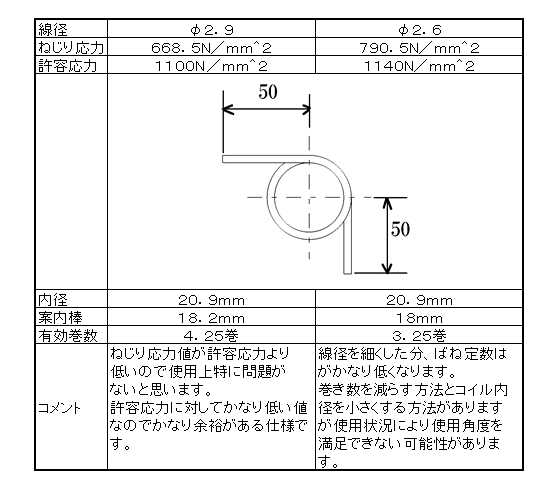
仮に、線径2.9mm・内径20mmで計算します。
まず、中心トルクを計算します。本来、荷重点からコイル中心までの距離で中心トルクを算出しますが、近似値で話を進めます。
荷重点のアーム長が50mmであり、荷重点の荷重が32Nなので中心トルクは
中心トルク = 50mm × 32N = 1600N・mm
ばね定数を求めます。
使用角度45度で1600N・mmの中心トルクとなりますので
ばね定数 = 使用角度時の中心トルク ÷ 使用角度
= 1600 ÷ 45
= 35.5 N・mm/度
前述の計算式アーム長さを考慮するか否かの目安より(アーム長さ1+アーム長さ2)≧0.09×π×D×Nの条件を満たすのでアーム長さを考慮しない場合で話を進めます。
ばね定数の計算式
ばね定数 = (E×線径^4)÷(3667×D×N) より
巻き数を逆算します。
この時の縦弾性係数「E」は186000、コイル平均径は22.9になります。
N = (E×2.9^4)÷(3667×22.9×35.5)
= 4.41 巻
自由角度が90度なので巻き数を調整します。4.25巻きとなります。
ばね定数が少し大きくなるので内径を少し大きくし、ばね定数を合わせます。
内径20.9mmとしました。
案内棒の計算をします。
△D = φdmax÷(360×N)×D
= 45÷(360×4.25)×23.8
= 0.7mm
案内棒の直径 = 0.9×(20.9-0.7)
= 18.2mm
曲げ応力 = (32×使用時のトルク)÷(π×線径^3)
= (32×1,600)÷(3.14×2.9^3)
= 668.5N/mm^2
= 668.5N/mm^2
「応力のとり方」文中の図1より許容ねじり応力は、1,100N/mm^2になります。
許容応力よりかなり低いので特に問題がない充分満足できる仕様と思われます。
線径をJISの規格線径の一つ細いもので計算してみます。線径を細くしたのでかなりばね定数が下がってしまいます。
その為、巻き数を1巻減らして計算しました。
線径を2.6φ・コイル内径20.9mm・巻き数を3.25巻きにすると下記ばね定数になります。
ばね定数 = (E×2.6^4)÷(3667×23.5×3.25)
= 30.3N・mm/度
線径2.9φに比べばね定数が低くなっております。
案内棒の計算をします。
△D = φdmax÷(360×N)×D
= 45÷(360×3.25)×23.5
= 0.9mm
案内棒の直径 = 0.9×(20.9―0.9)
= 18.2mm
中心トルク = ばね定数 × 使用角度
= 30.3 × 45
= 1,363.5N・mm
曲げ応力 = (32×使用時のトルク)÷(π×線径^3)
= (32×1363.5)÷(3.14×2.6^3)
= 790.5N/mm^2
= 790.5N/mm^2
「応力のとり方」文中の図1より許容ねじり応力は、1,140N/mm^2になります。
ばねの軽量化にはなりました。ばね定数は線径を細くした分下がっております。
ばね定数を2.9φに近づけるには、コイル径を小さくする方法と巻き数を減らす方法があります。
但しその場合、使用角度を満足できない可能性もあります。
設計時は、このような両側面を考慮する必要があります。




