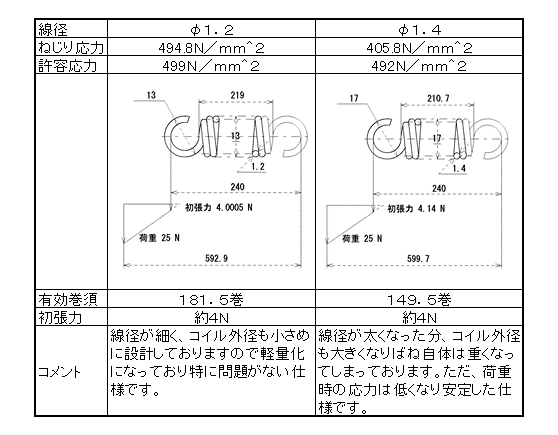
下記にて設計計算事例の詳細を示します。
仮に線径1.2mm・外径13mmで計算します。
この時の横弾性係数「G」は68,500、コイル平均径は11.8mmになります。
有効巻数を計算します。
コイル平均径11.8mmよりコイル内径は10.4mmとなります。
フックの内径となります。自由長さ240mmとなっておりますのでコイル
胴体部長さは、自由長 ― コイル内径 × 2より
胴体部長さ = 240―10.4×2 = 219.2
有効巻数 = 胴体部長さ ÷ 線径 -1 = 181.666
引張ばねの場合、一般的にフックのスキマを互い違いにする事が多い為、巻き数を181.5にします。
有効巻数 = 181.5 巻となります。
ばね定数は計算式より
k = (G×1.2^4)/(8×181.5×11.8^3)
= 0.0595N/mm
引張ばねの場合、初張力が付きます。上記の計算式より求めます。
Cはばね指数で今回は9.8
初応力 = G / (100×C)=68500/(100×9.8)
= 69.9
初張力 = (π×d^3)/(8×D)×初応力
= 4.01N
ねじり応力(静荷重使用)を計算します。
ねじり応力 = (8×D×P)÷(π×d^3)
= (8×11.8×25)÷(3.14×1.2^3)
= 434N/mm^2
応力修正係数 =(4×C-1)÷(4×C-4)+
0.615÷C
=(4×9.8-1)÷(4×9.8-4)+
0.615÷9.8
= 1.14
ねじり修正応力(静荷重使用)= 応力修正係数×ねじり応力
1.14 × 434
= 494.8N/mm^2
「応力のとり方」文中の図1より許容ねじり応力は780N/mm^2)になります。
常用応力としてこの値の64%以下にとるのが望ましいので
許容ねじり応力 = 780 × 0.64 =499N/mm^2
特に問題がない仕様と思われます。
同じ条件で、もう少し荷重時の応力を下げるべく線径をJISの規格線径の一つ太いもの計算してみます。
引張ばねの場合、線径が太くなると自由長が決まっていますので、胴体部の長さより巻き数が少なることになります。
また、ばね定数もコイル平均径が小さくなる為ばね定数・初張力が高くなります。
コイル平均径を大きくし、ばね定数・初張力を調整します。
今回は、仮に外径17mmとします。
有効巻数を計算します。
コイル平均径15.6mmよりコイル内径は14.2mmとなります。
フックの内径となります。自由長さ240mmとなっておりますのでコイル
胴体部長さは、自由長 ― コイル内径 × 2より
胴体部長さ = 240―14.2×2 = 211.6
有効巻数 = 胴体部長さ÷線径-1 = 150.1
線径1.2mmと同じように巻き数を.5にします。但し今回は150.5巻にすると計算上自由長が長くなってしますので下記巻き数に修正します。
有効巻数 = 149.5 巻となります。
ばね定数は計算式より
k = (G×1.4^4)/(8×149.5×15.6^3)
= 0.058N/mm
線径1.2mmと同じようなばね定数になりました。
引張ばねの場合、初張力が付きます。上記の計算式より求めます。
Cは、ばね指数で今回は11.1
初応力 = G/(100×C)=68500/(100×11.1)
= 61.7
初張力 = (π×d^3)/(8×D)×初応力
= 4.25N
ねじり応力(静荷重使用)を計算します。
ねじり応力=(8×D×P)÷(π×d^3)
=(8×15.6×25)÷(3.14×1.4^3)
=362N/mm^2
応力修正係数=(4×C-1)÷(4×C-4)+
0.615÷C
=(4×11.1-1)÷(4×11.1-4)+
0.615÷11.1
=1.12
ねじり修正応力(静荷重使用)=応力修正係数×ねじり応力
1.12 × 362
=405.84N/mm^2
「応力のとり方」文中の図1より許容ねじり応力は780N/mm^2)になります。
常用応力としてこの値の64%以下にとるのが望ましいので
許容ねじり応力 = 770×0.64 =492N/mm^2
線径1.4mmの方が、1.2mmのときより許容応力に対して低くなり安定した仕様と思われます。
但し、コイルの径が大きくなるので相手部品とのかみ合わせで支障がでる可能があります。
このように設計時には両側面を考慮する必要性があります。




